Loading...
Back to:
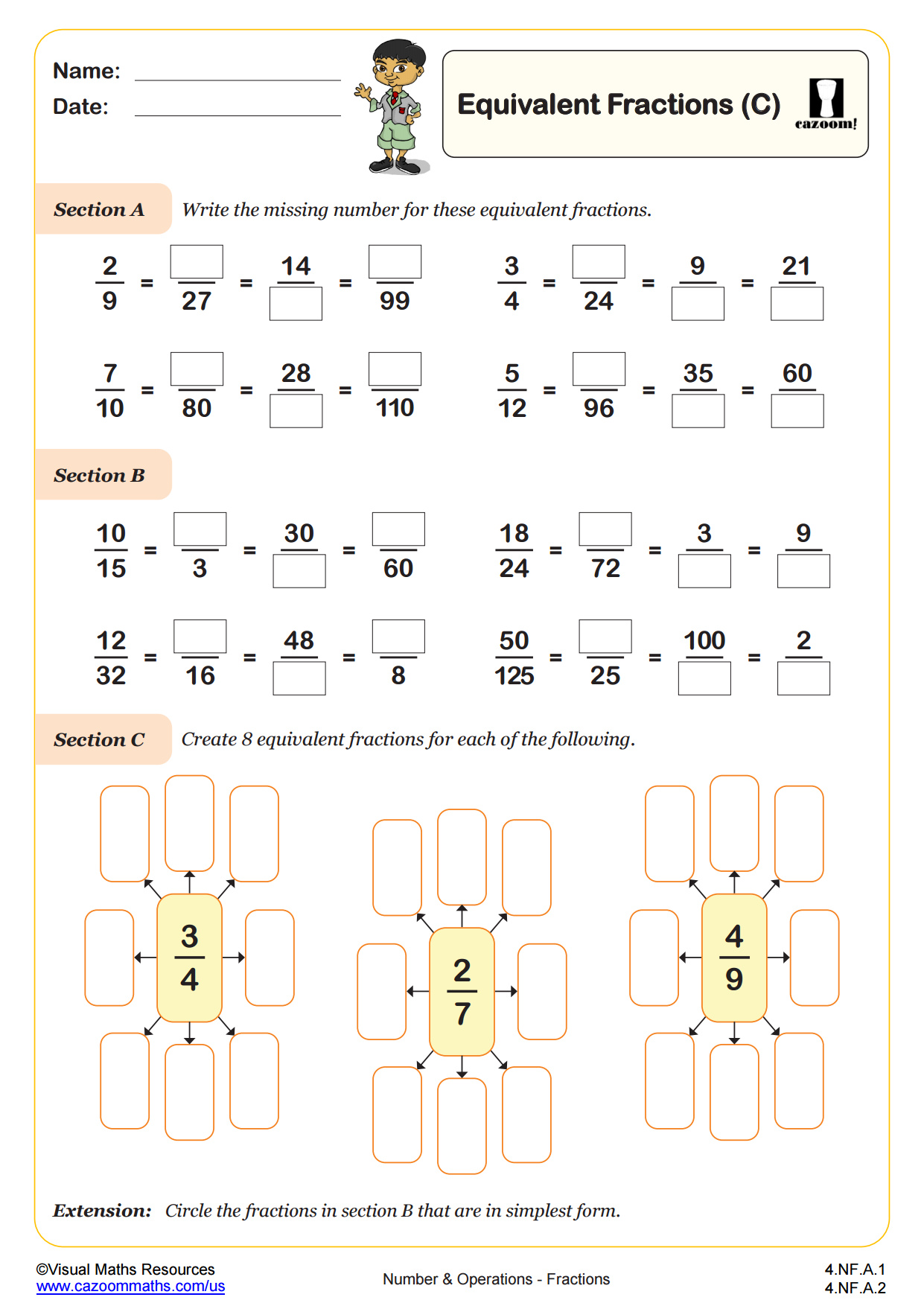
Equivalent Fractions (C) WORKSHEET
Suitable for Grades: 4th Grade
CCSS: 4.NF.A.1, 4.NF.A.2
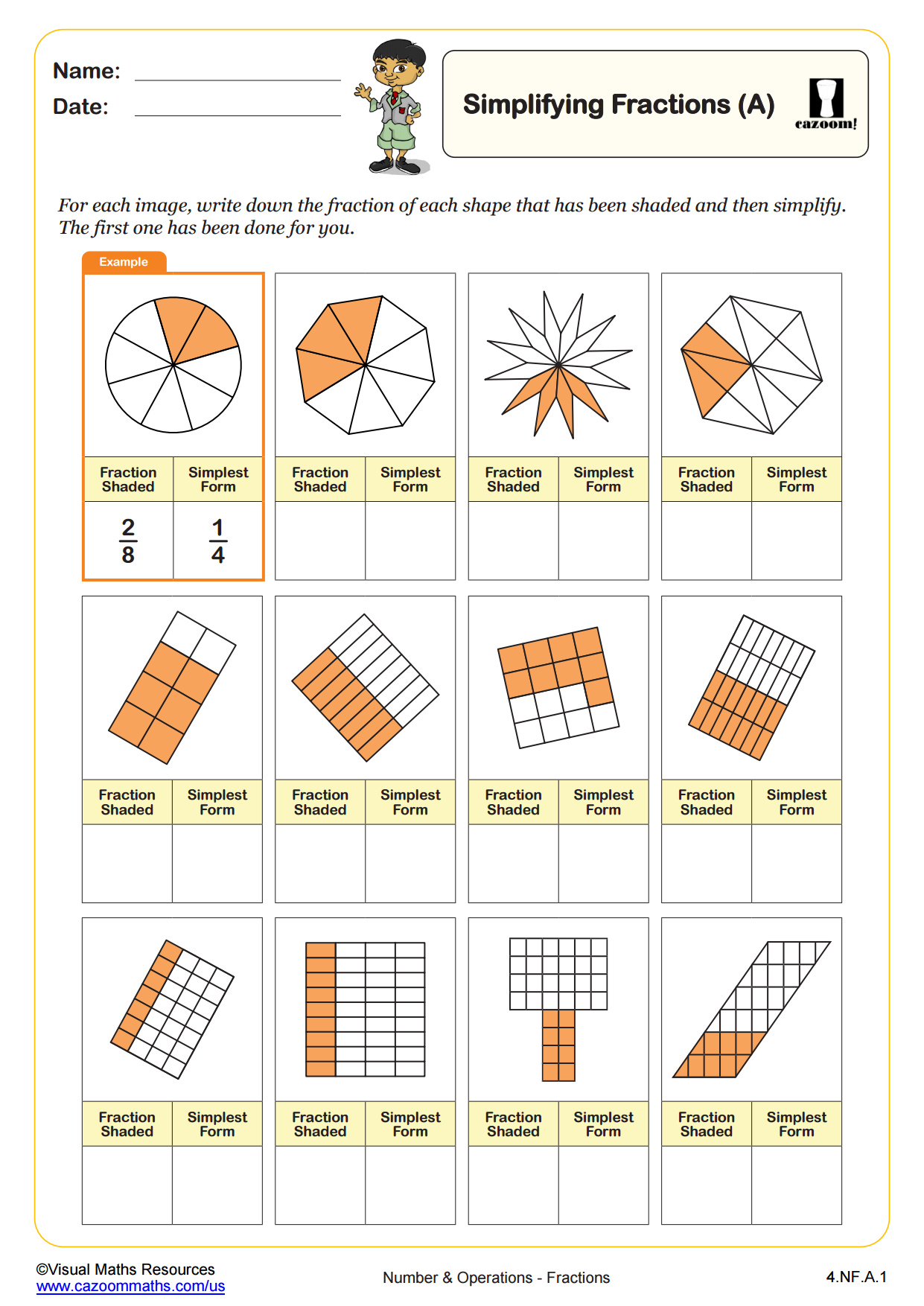
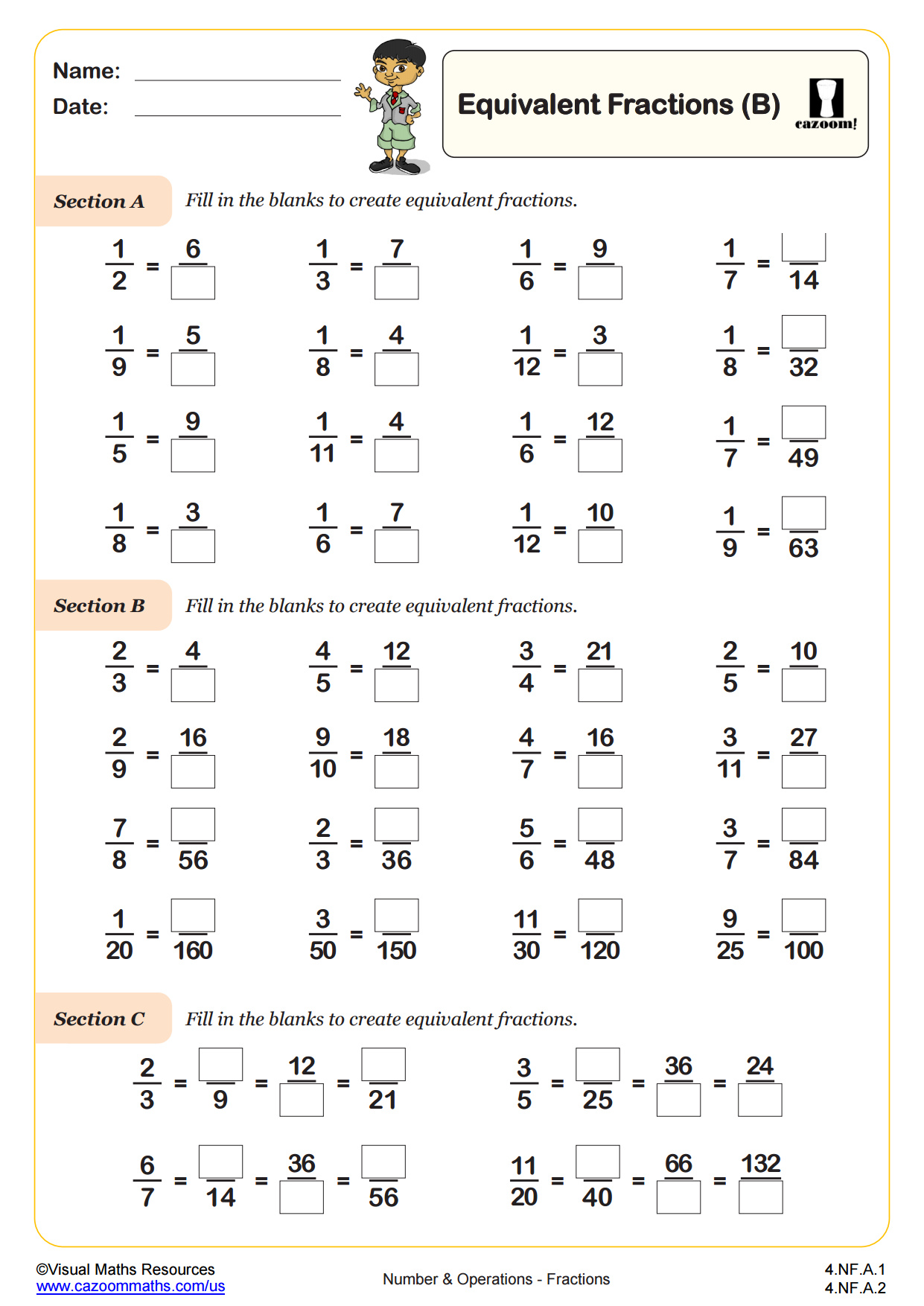
CCSS Description: Explain why a fraction a/b is equivalent to a fraction (n × a)/(n × b) by using visual fraction models, with attention to how the number and size of the parts differ even though the two fractions themselves are the same size. Use this principle to recognize and generate equivalent fractions.
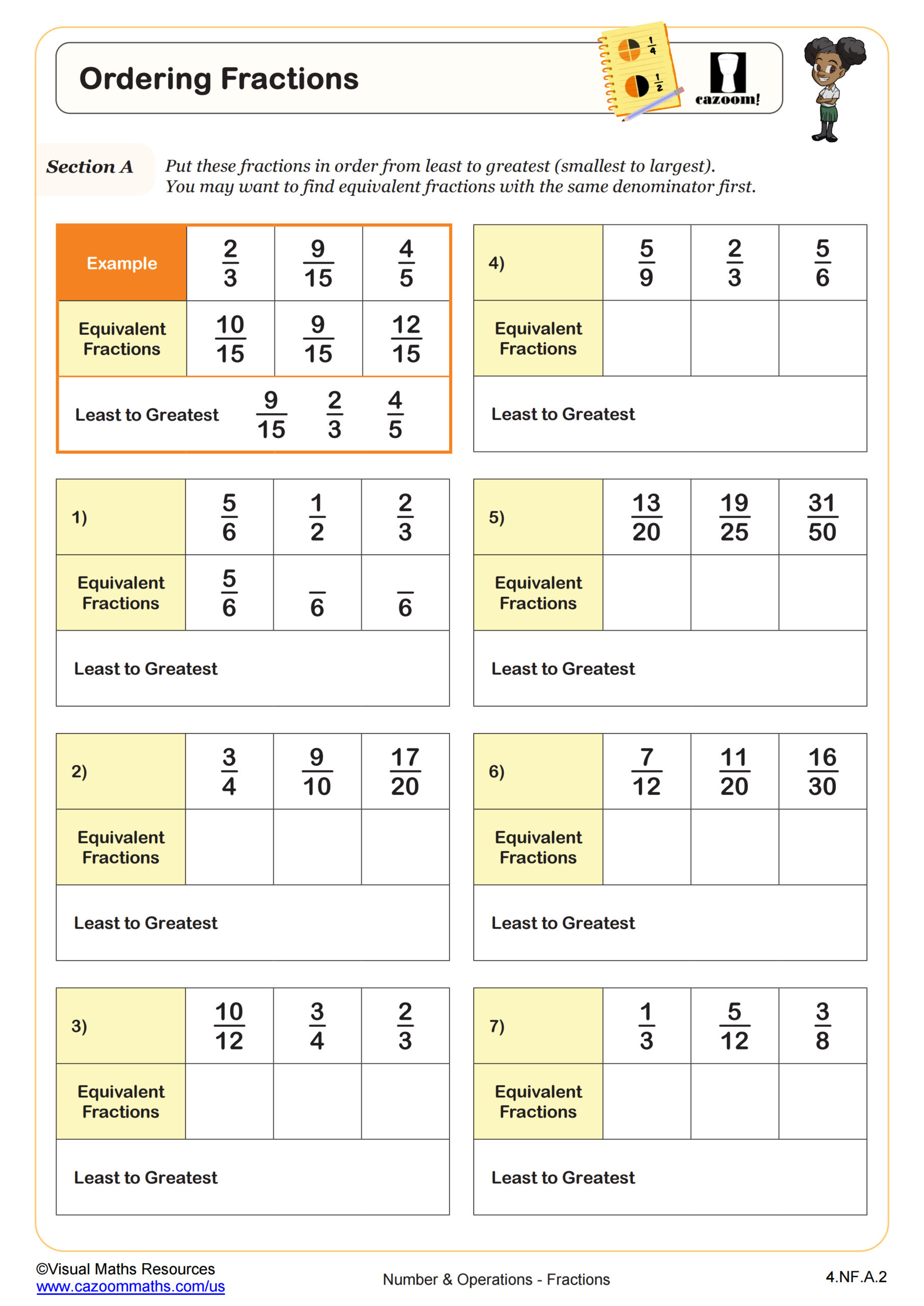
Compare two fractions with different numerators and different denominators, e.g., by creating common denominators or numerators, or by comparing to a benchmark fraction such as 1/2. Recognize that comparisons are valid only when the two fractions refer to the same whole. Record the results of comparisons with symbols >, =, or <, and justify the conclusions, e.g., by using a visual fraction model.
Compare two fractions with different numerators and different denominators, e.g., by creating common denominators or numerators, or by comparing to a benchmark fraction such as 1/2. Recognize that comparisons are valid only when the two fractions refer to the same whole. Record the results of comparisons with symbols >, =, or <, and justify the conclusions, e.g., by using a visual fraction model.
Equivalent Fractions (C) WORKSHEET DESCRIPTION
Begin finding equivalent fractions of unit fractions in this worksheet with either a numerator or denominator given. Section A sees students finding four fractions equivalent to one half, one third, one forth and one fifth. While section B is similar, it gives an opportunity for discussion as students see how fractions with the same numerator can be equivalent to one half, one third, one forth or one fifth. Challenge learners in section C, with a string of equivalent fractions to extend learning.