Loading...
Graphing Inequalities (B) WORKSHEET
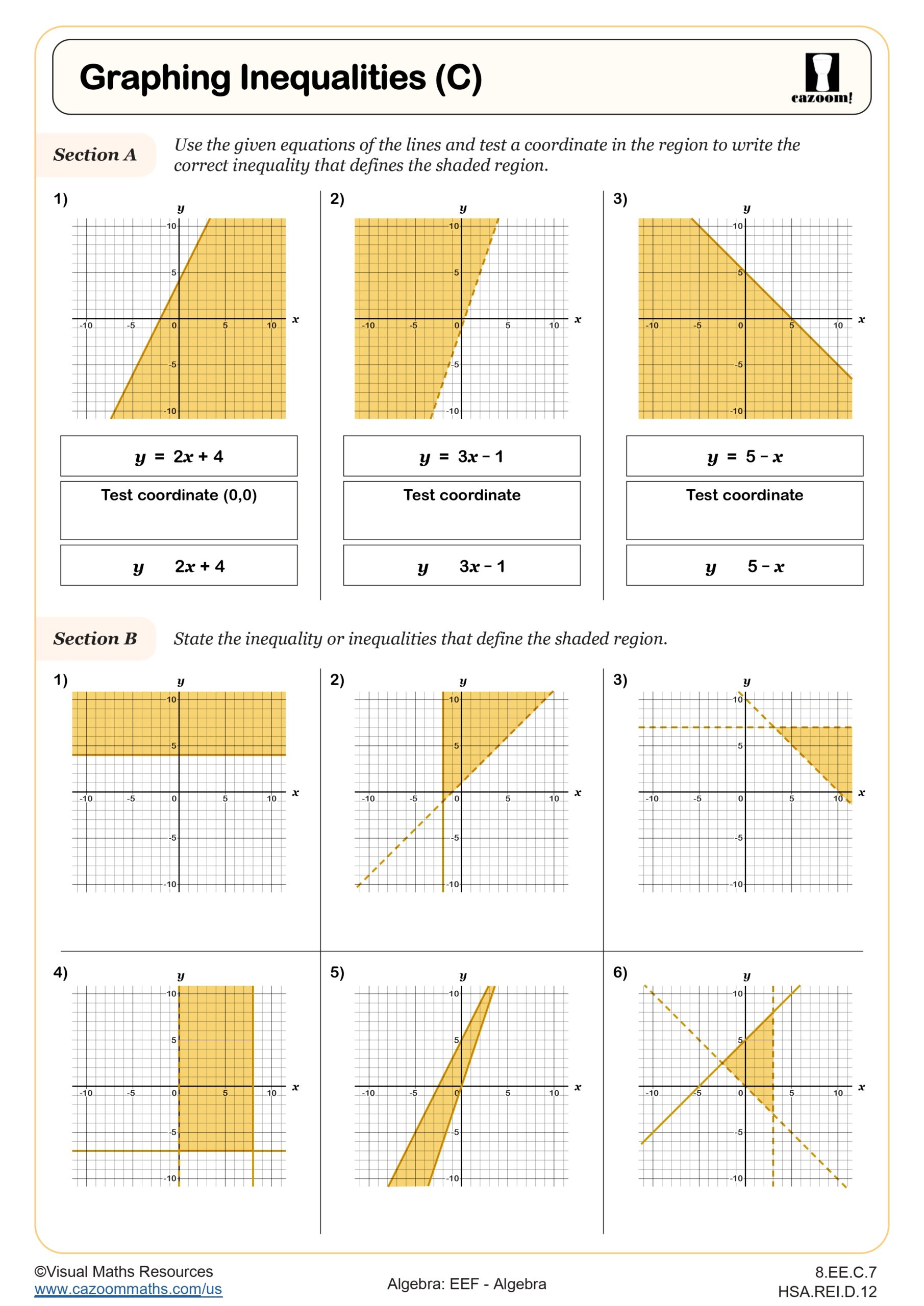
Graph the solutions to a linear inequality in two variables as a half-plane (excluding the boundary in the case of a strict inequality), and graph the solution set to a system of linear inequalities in two variables as the intersection of the corresponding half-planes.
Graphing Inequalities (B) WORKSHEET DESCRIPTION
Students will graph single linear inequalities throughout this worksheet.
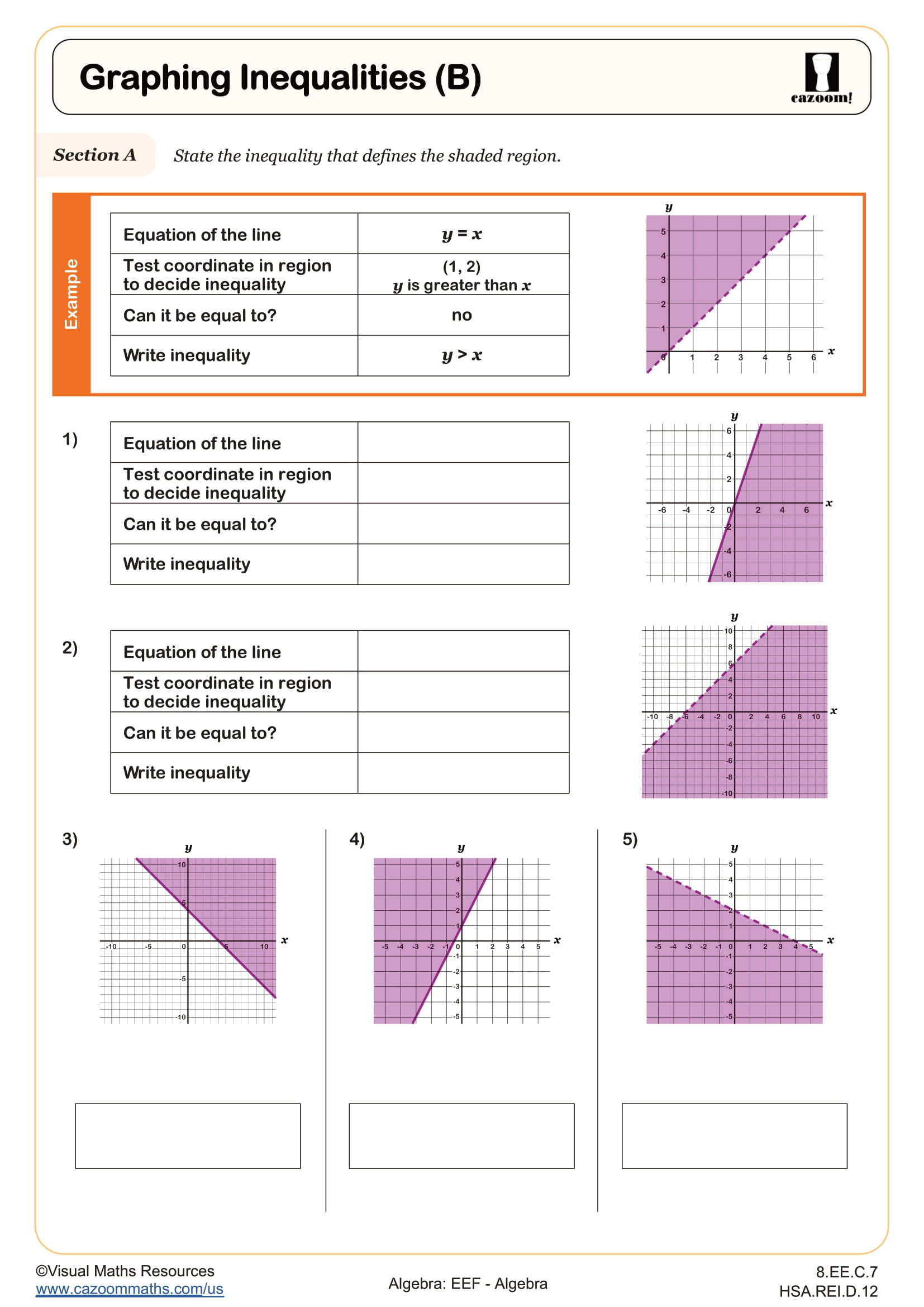
In Section A learners are reminded to find the equation of line that defines the region and to use a test coordinate inside the region to determine the inequality. After seeing an example they will repeat this process over five questions.
Next students are asked to graph nine different linear inequalities on separate pre-drawn coordinate grids in Section B. Students are required to plot graphs in the form y = mx + c with positive and negative values of m and c before using a test coordinate again to choose the region that satisfies the inequality.
Need an extra challenge? Check out Graphing Inequalities (C) which sees learners defining regions determined by two or three inequalities.