Loading...
Back to:
Graphing Relationships (A) - Drawing and Interpreting WORKSHEET
Suitable for Grades: 6th Grade, 8th Grade
CCSS: 6.EE.C.9, 8.F.B.4
CCSS Description: Use variables to represent two quantities in a real-world problem that change in relationship to one another; write an equation to express one quantity, thought of as the dependent variable, in terms of the other quantity, thought of as the independent variable. Analyze the relationship between the dependent and independent variables using graphs and tables, and relate these to the equation. For example, in a problem involving motion at constant speed, list and graph ordered pairs of distances and times, and write the equation d = 65t to represent the relationship between distance and time.
Construct a function to model a linear relationship between two quantities. Determine the rate of change and initial value of the function from a description of a relationship or from two (x, y) values, including reading these from a table or from a graph. Interpret the rate of change and initial value of a linear function in terms of the situation it models, and in terms of its graph or a table of values.
Construct a function to model a linear relationship between two quantities. Determine the rate of change and initial value of the function from a description of a relationship or from two (x, y) values, including reading these from a table or from a graph. Interpret the rate of change and initial value of a linear function in terms of the situation it models, and in terms of its graph or a table of values.
Graphing Relationships (A) - Drawing and Interpreting WORKSHEET DESCRIPTION
This worksheet focuses on the practical application of drawing and interpreting charge graphs and exposes learners to various different ‘cost’ scenarios; designed to develop students' abilities to interpret and construct linear graphs, understand proportional relationships, and apply mathematical reasoning to solve practical problems.
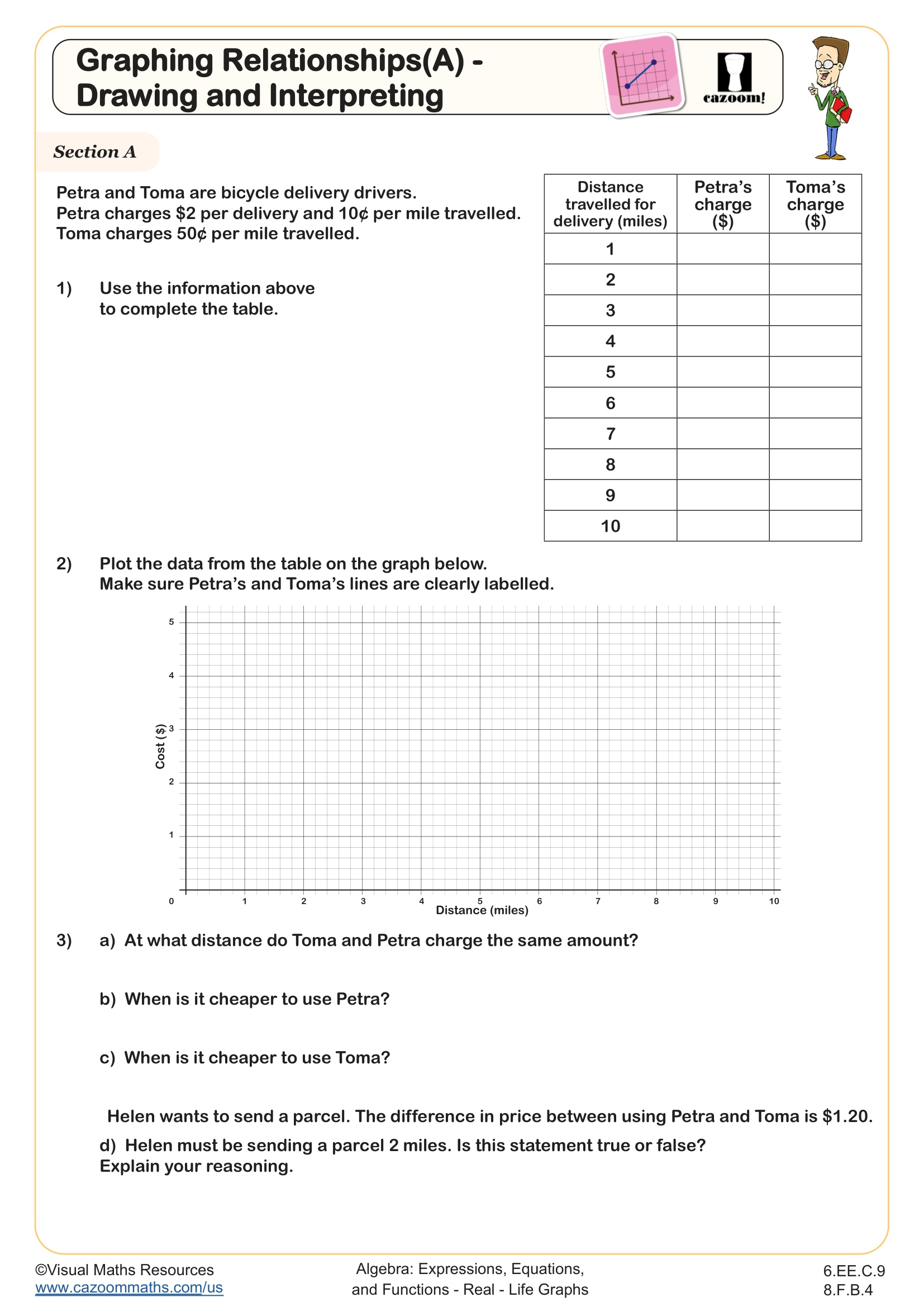
Students will begin by completing a table using given pricing information, plotting the data and answering questions in order to compare the charges of two bicycle delivery services in section A.
Then, section B will see students matching multiple electricity companies charges to the correct charge graphs.
Students will draw four different charge graphs in section C.
Lastly, section D provides more opportunity to interpret charge graphs as learners answer questions about costs.
