Loading...
Back to:
Graphing Relationships (B) - Equations WORKSHEET
Suitable for Grades: 6th Grade, 8th Grade
CCSS: 6.EE.C.9, 8.F.B.4
CCSS Description: Use variables to represent two quantities in a real-world problem that change in relationship to one another; write an equation to express one quantity, thought of as the dependent variable, in terms of the other quantity, thought of as the independent variable. Analyze the relationship between the dependent and independent variables using graphs and tables, and relate these to the equation. For example, in a problem involving motion at constant speed, list and graph ordered pairs of distances and times, and write the equation d = 65t to represent the relationship between distance and time.
Construct a function to model a linear relationship between two quantities. Determine the rate of change and initial value of the function from a description of a relationship or from two (x, y) values, including reading these from a table or from a graph. Interpret the rate of change and initial value of a linear function in terms of the situation it models, and in terms of its graph or a table of values.
Construct a function to model a linear relationship between two quantities. Determine the rate of change and initial value of the function from a description of a relationship or from two (x, y) values, including reading these from a table or from a graph. Interpret the rate of change and initial value of a linear function in terms of the situation it models, and in terms of its graph or a table of values.
Graphing Relationships (B) - Equations WORKSHEET DESCRIPTION
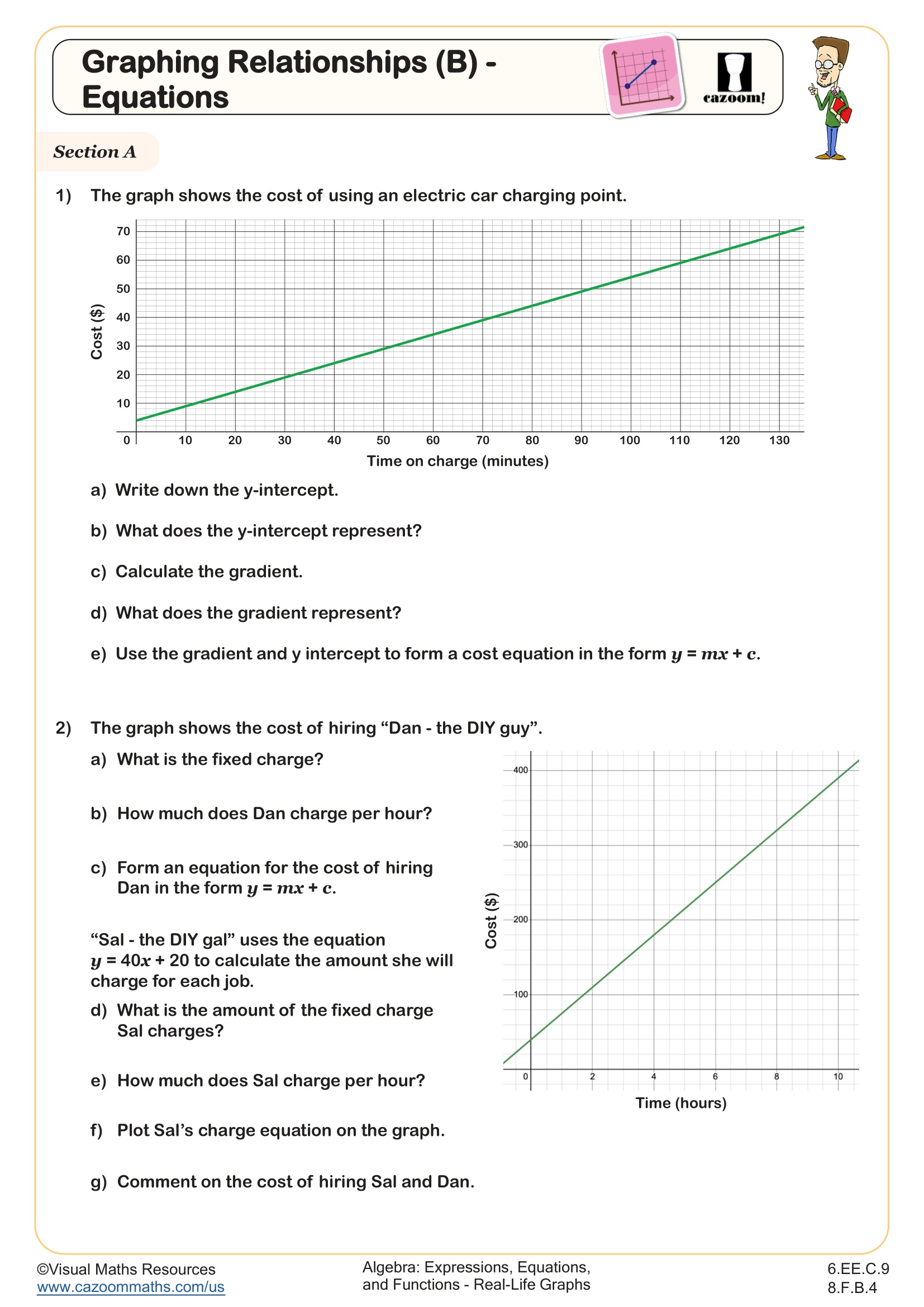
Enhance students' ability to interpret graphs with this worksheet, which connects real-life graphs to linear functions in the form y = mx + c. Learners will find the equations of straight lines and understand how the y-intercept and gradient represent a fixed charge and charge per unit in section A. This section leads students to match linear equations with charge scenarios and their corresponding graphs in section B. Finally, students will form equations themselves from scenarios such as, “A taxi company charges a fixed fee of $3.70 and 70 ¢ per mile.” This approach helps reinforce their understanding of how linear functions apply to real-world situations.