Loading...
Back to:
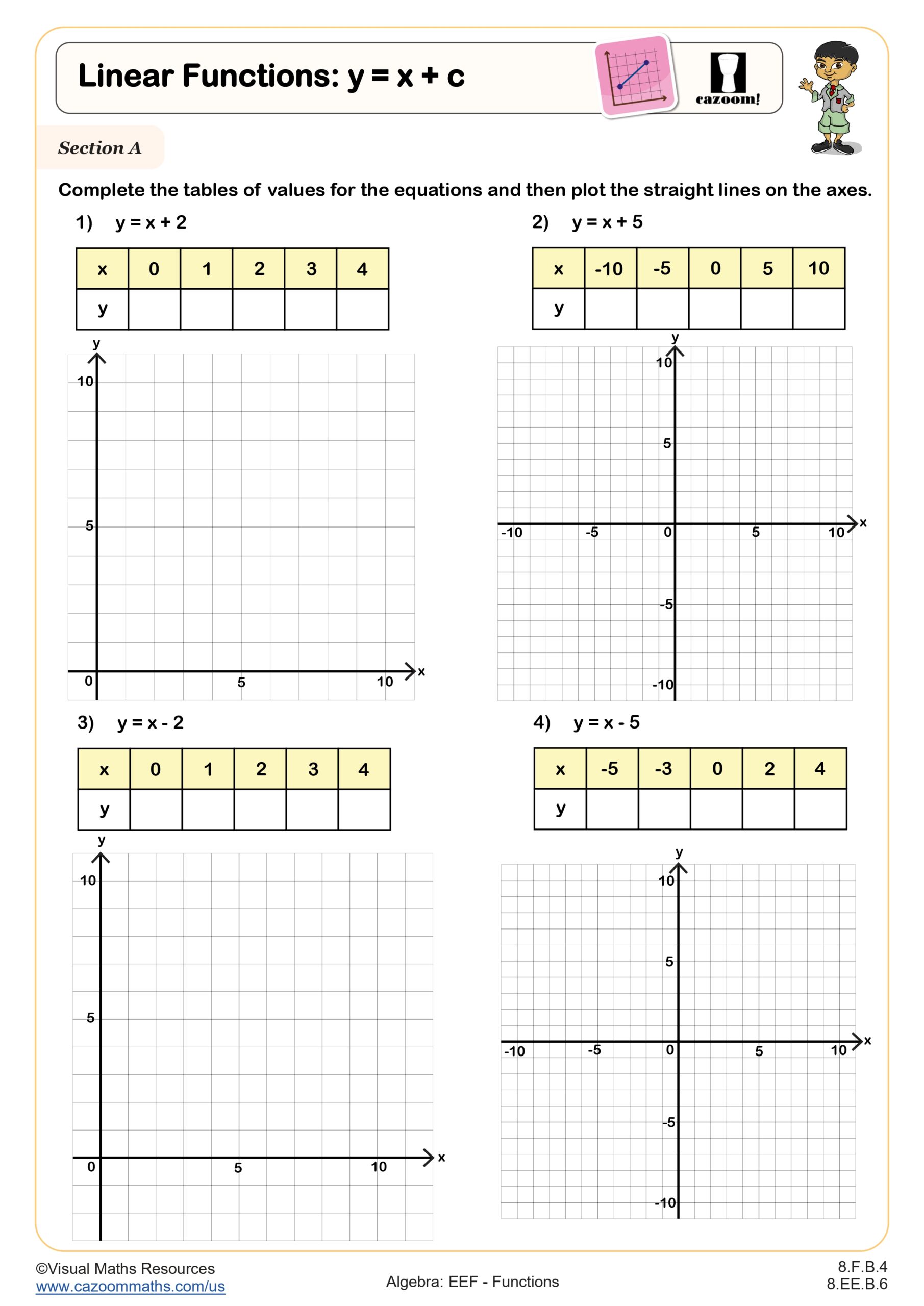
Linear Functions: y = x + c WORKSHEET
Suitable for Grades: 8th Grade
CCSS: 8.EE.B.6, 8.F.B.4
CCSS Description: Use similar triangles to explain why the slope m is the same between any two distinct points on a non-vertical line in the coordinate plane; derive the equation y = m x for a line through the origin and the equation y = m x + b for a line intercepting the vertical axis at b.
Construct a function to model a linear relationship between two quantities. Determine the rate of change and initial value of the function from a description of a relationship or from two (x, y) values, including reading these from a table or from a graph. Interpret the rate of change and initial value of a linear function in terms of the situation it models, and in terms of its graph or a table of values.
Construct a function to model a linear relationship between two quantities. Determine the rate of change and initial value of the function from a description of a relationship or from two (x, y) values, including reading these from a table or from a graph. Interpret the rate of change and initial value of a linear function in terms of the situation it models, and in terms of its graph or a table of values.
Linear Functions: y = x + c WORKSHEET DESCRIPTION
This worksheet on linear functions provides an exploration of graphing and interpreting straight lines in the form y = x + c.
In Section A, learners will complete tables of values for linear equations and plot them on graphs.
Section B challenges students to identify y-intercepts and write the corresponding linear equations, reinforcing their understanding of how changes in equations affect graphs. Section C builds on this by having students use tables of values to derive equations.
Finally, Section D pushes students further, asking them to find the equations of lines passing through three pairs of points, encouraging problem-solving and application of key concepts.