Loading...
Back to:
Multiplying and Dividing Fractions WORKSHEET
Suitable for Grades: 5th Grade, 6th Grade
CCSS: 5.NF.B.4, 6.NS.A.1
CCSS Description: Apply and extend previous understandings of multiplication to multiply a fraction or whole number by a fraction. a. Interpret the product (a/b) × q as a parts of a partition of q into b equal parts; equivalently, as the result of a sequence of operations a × q ÷ b. For example, use a visual fraction model to show (2/3) × 4 = 8/3, and create a story context for this equation. Do the same with (2/3) × (4/5) = 8/15. (In general, (a/b) × (c/d) = ac/bd.) b. Find the area of a rectangle with fractional side lengths by tiling it with unit squares of the appropriate unit fraction side lengths, and show that the area is the same as would be found by multiplying the side lengths. Multiply fractional side lengths to find areas of rectangles, and represent fraction products as rectangular areas.
Interpret and compute quotients of fractions, and solve word problems involving division of fractions by fractions, e.g., by using visual fraction models and equations to represent the problem. For example, create a story context for (2/3) ÷ (3/4) and use a visual fraction model to show the quotient; use the relationship between multiplication and division to explain that (2/3) ÷ (3/4) = 8/9 because 3/4 of 8/9 is 2/3. (In general, (a/b) ÷ (c/d) = ad/bc.) How much chocolate will each person get if 3 people share 1/2 lb of chocolate equally? How many 3/4-cup servings are in 2/3 of a cup of yogurt? How wide is a rectangular strip of land with length 3/4 mi and area 1/2 square mi?
Interpret and compute quotients of fractions, and solve word problems involving division of fractions by fractions, e.g., by using visual fraction models and equations to represent the problem. For example, create a story context for (2/3) ÷ (3/4) and use a visual fraction model to show the quotient; use the relationship between multiplication and division to explain that (2/3) ÷ (3/4) = 8/9 because 3/4 of 8/9 is 2/3. (In general, (a/b) ÷ (c/d) = ad/bc.) How much chocolate will each person get if 3 people share 1/2 lb of chocolate equally? How many 3/4-cup servings are in 2/3 of a cup of yogurt? How wide is a rectangular strip of land with length 3/4 mi and area 1/2 square mi?
Multiplying and Dividing Fractions WORKSHEET DESCRIPTION
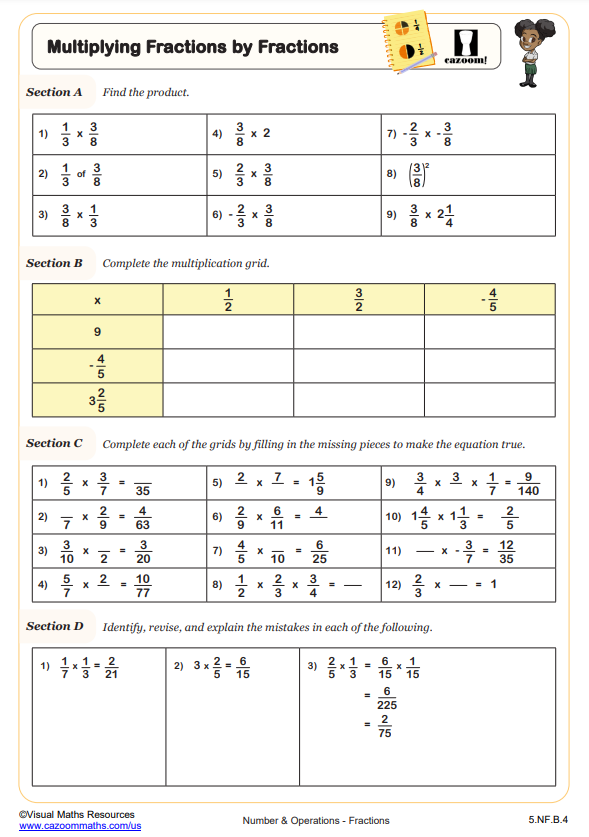
Ensure students are secure in multiplying and dividing fractions with this worksheet, which will see them alternating between the two operations.
In section A, learners will multiply fractions and integers. Answers may need simplifying and are given as improper fractions.
Multiply pairs of fractions in section B. Again, students will need to watch out for any answers that need to be simplified as they go.
Students must consider the nuance in the order of fractions and integers they are dividing in section C.
Section D brings some variation in questioning as students see division of fractions as a fraction over a fraction!
Finally, learners will multiply and divide fractions and mixed numbers in section E.