Loading...
Back to:
Recipe Proportions (A) WORKSHEET
Suitable for Grades: 6th Grade, 7th Grade
CCSS: 6.RP.A.1, 7.RP.A.2
CCSS Description: Understand the concept of a ratio and use ratio language to describe a ratio relationship between two quantities. For example, “The ratio of wings to beaks in the bird house at the zoo was 2:1, because for every 2 wings there was 1 beak.” “For every vote candidate A received, candidate C received nearly three votes.”
Recognize and represent proportional relationships between quantities. a. Decide whether two quantities are in a proportional relationship, e.g., by testing for equivalent ratios in a table or graphing on a coordinate plane and observing whether the graph is a straight line through the origin. b. Identify the constant of proportionality (unit rate) in tables, graphs, equations, diagrams, and verbal descriptions of proportional relationships. c. Represent proportional relationships by equations. For example, if total cost t is proportional to the number n of items purchased at a constant price p, the relationship between the total cost and the number of items can be expressed as t = pn. d. Explain what a point (x, y) on the graph of a proportional relationship means in terms of the situation, with special attention to the points (0, 0) and (1, r) where r is the unit rate.
Recognize and represent proportional relationships between quantities. a. Decide whether two quantities are in a proportional relationship, e.g., by testing for equivalent ratios in a table or graphing on a coordinate plane and observing whether the graph is a straight line through the origin. b. Identify the constant of proportionality (unit rate) in tables, graphs, equations, diagrams, and verbal descriptions of proportional relationships. c. Represent proportional relationships by equations. For example, if total cost t is proportional to the number n of items purchased at a constant price p, the relationship between the total cost and the number of items can be expressed as t = pn. d. Explain what a point (x, y) on the graph of a proportional relationship means in terms of the situation, with special attention to the points (0, 0) and (1, r) where r is the unit rate.
Recipe Proportions (A) WORKSHEET DESCRIPTION
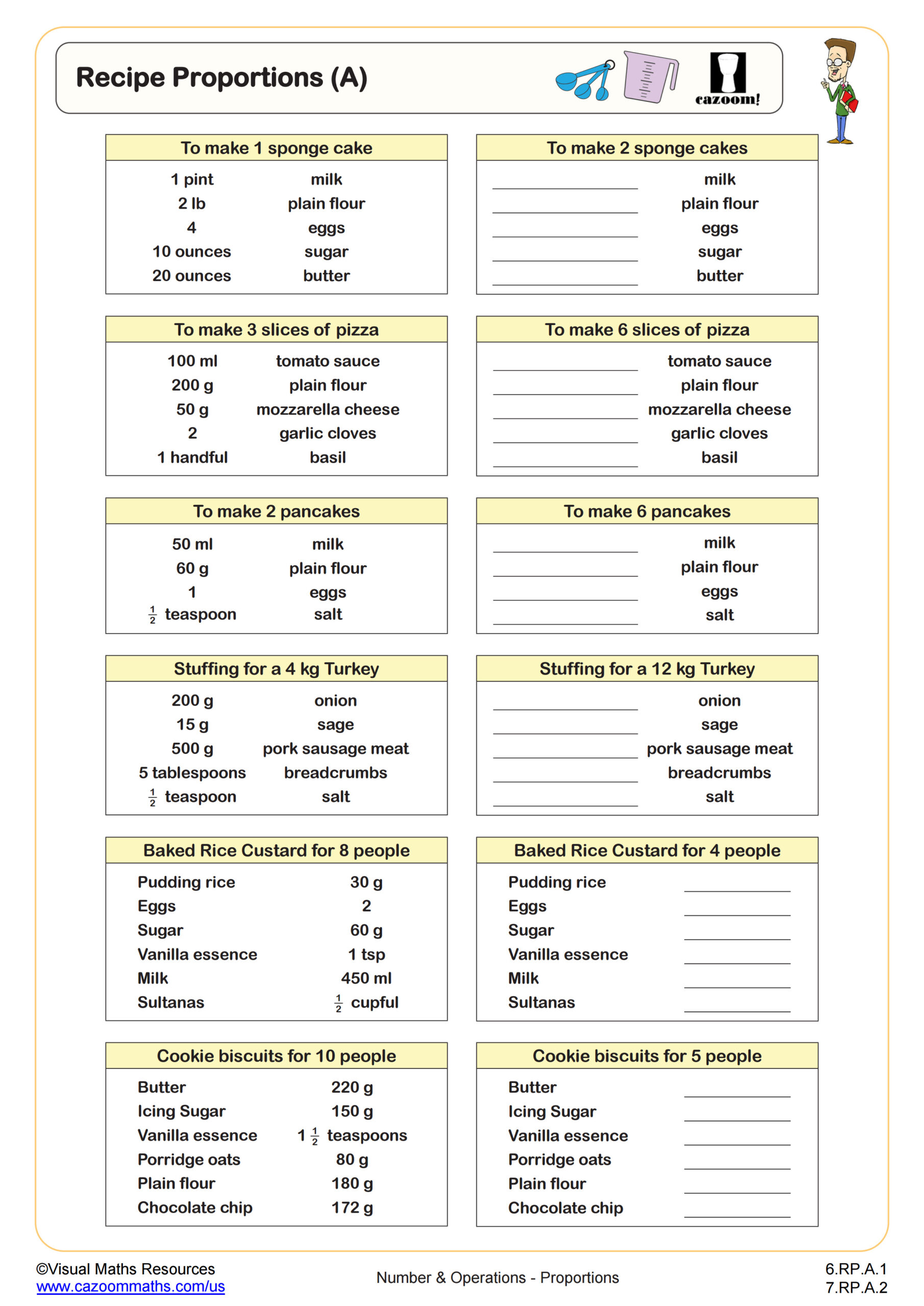
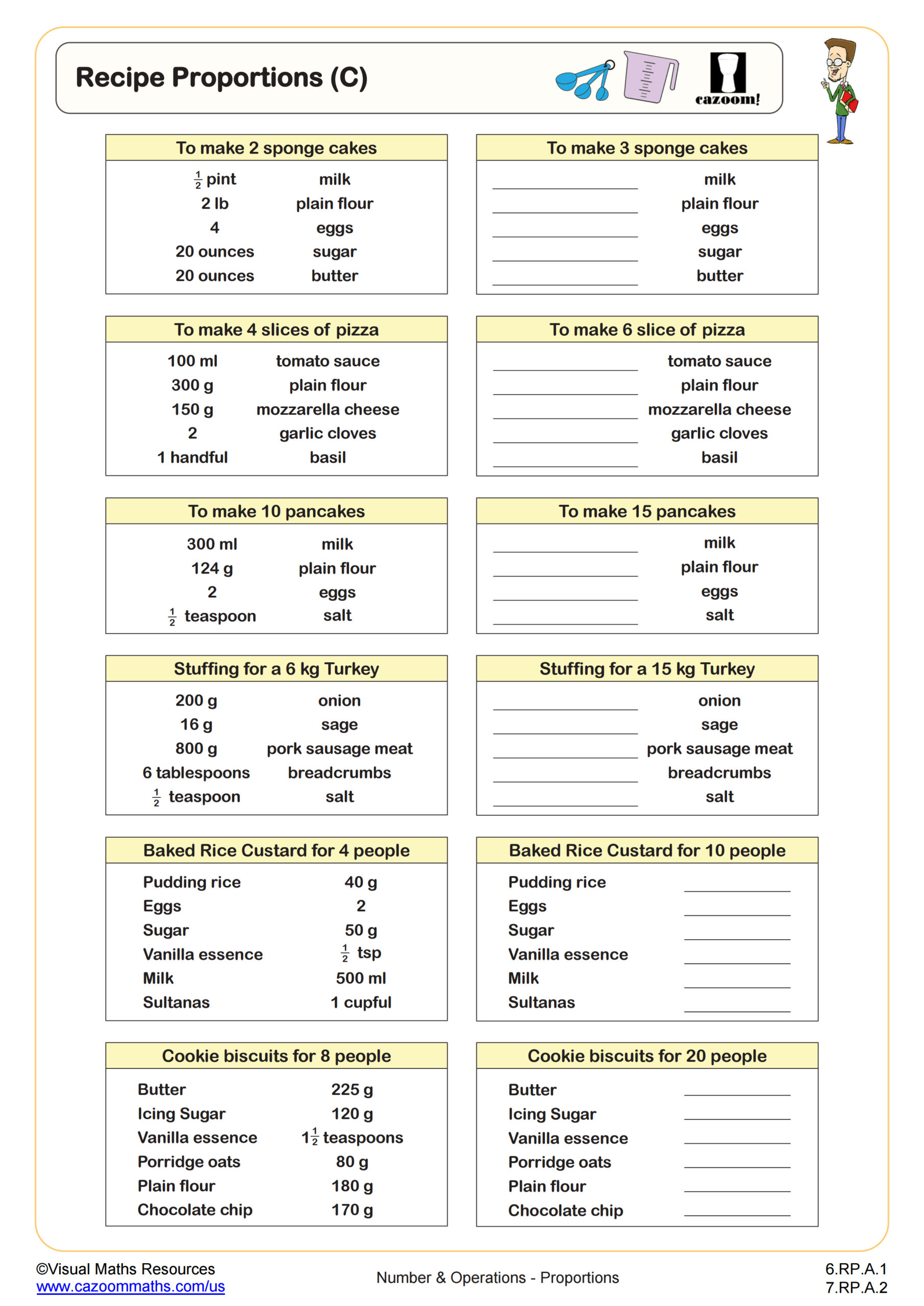
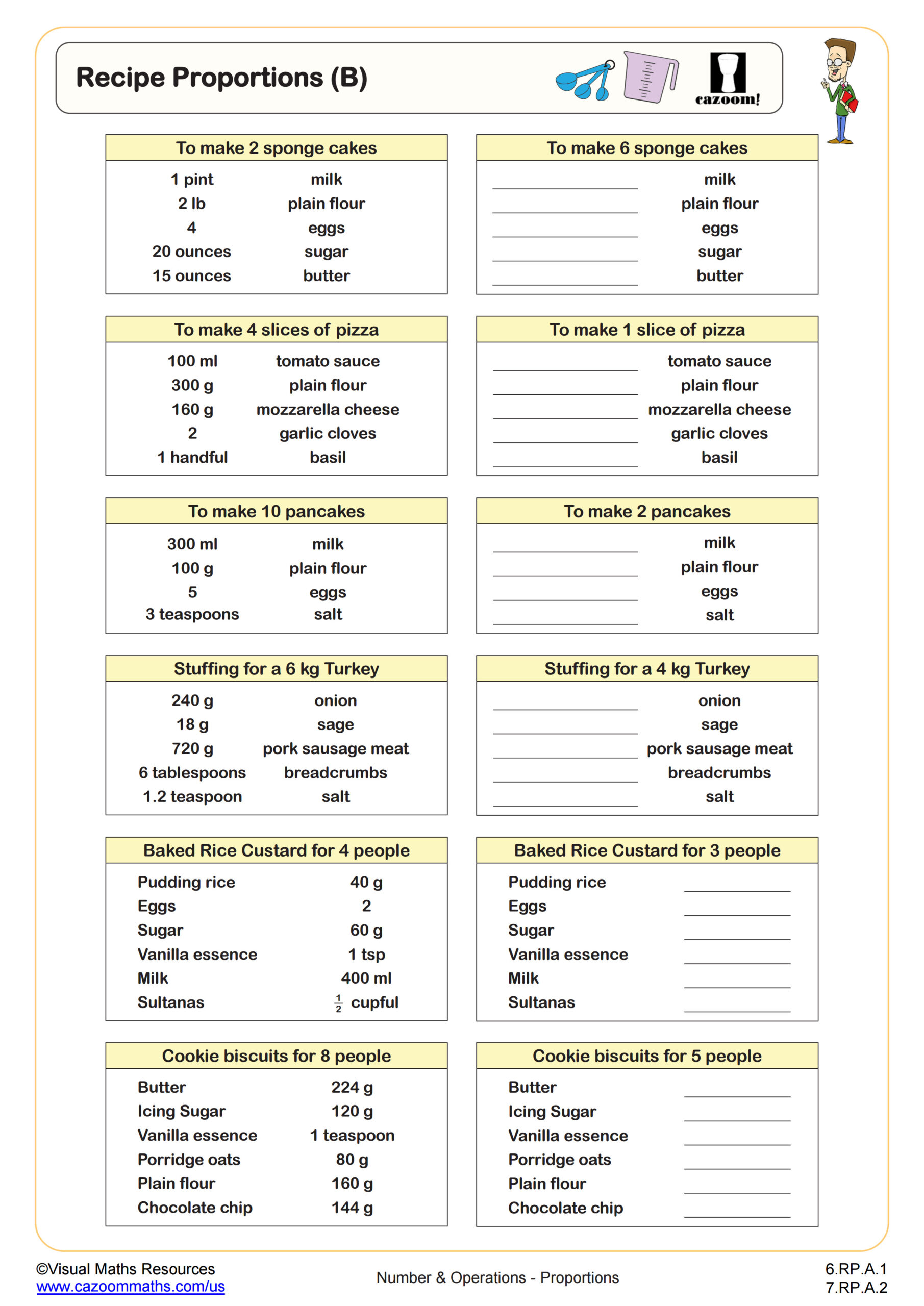
Recipe problems are the perfect conceptual introduction to direct proportion for many students. As long as learners are competent multipliers and dividers, they will be able to complete Recipes (A).
Here, students have 6 recipe cards to either scale up or down. To scale up, students may have to multiply ingredients by either 2 or 3, and to scale down, will be dividing by 2. However, learners will have to discover these scale factors for themselves.
Recipes (A) comes with the challenge of working with some fractional ingredients. For example, 1½ has to be halved and ½ has to be multiplied by 3.