Loading...
Back to:
The Probability Rule for Counting WORKSHEET
Suitable for Grades: 7th Grade, Algebra I, IM 1
CCSS: 7.SP.C.8, HSS.CP.A.5
CCSS Description: Find probabilities of compound events using organized lists, tables, tree diagrams, and simulation. a. Understand that, just as with simple events, the probability of a compound event is the fraction of outcomes in the sample space for which the compound event occurs. b. Represent sample spaces for compound events using methods such as organized lists, tables and tree diagrams. For an event described in everyday language (e.g., “rolling double sixes”), identify the outcomes in the sample space which compose the event. c. Design and use a simulation to generate frequencies for compound events. For example, use random digits as a simulation tool to approximate the answer to the question: If 40% of donors have type A blood, what is the probability that it will take at least 4 donors to find one with type A blood?
Recognize and explain the concepts of conditional probability and independence in everyday language and everyday situations. For example, compare the chance of having lung cancer if you are a smoker with the chance of being a smoker if you have lung cancer.
Recognize and explain the concepts of conditional probability and independence in everyday language and everyday situations. For example, compare the chance of having lung cancer if you are a smoker with the chance of being a smoker if you have lung cancer.
The Probability Rule for Counting WORKSHEET DESCRIPTION
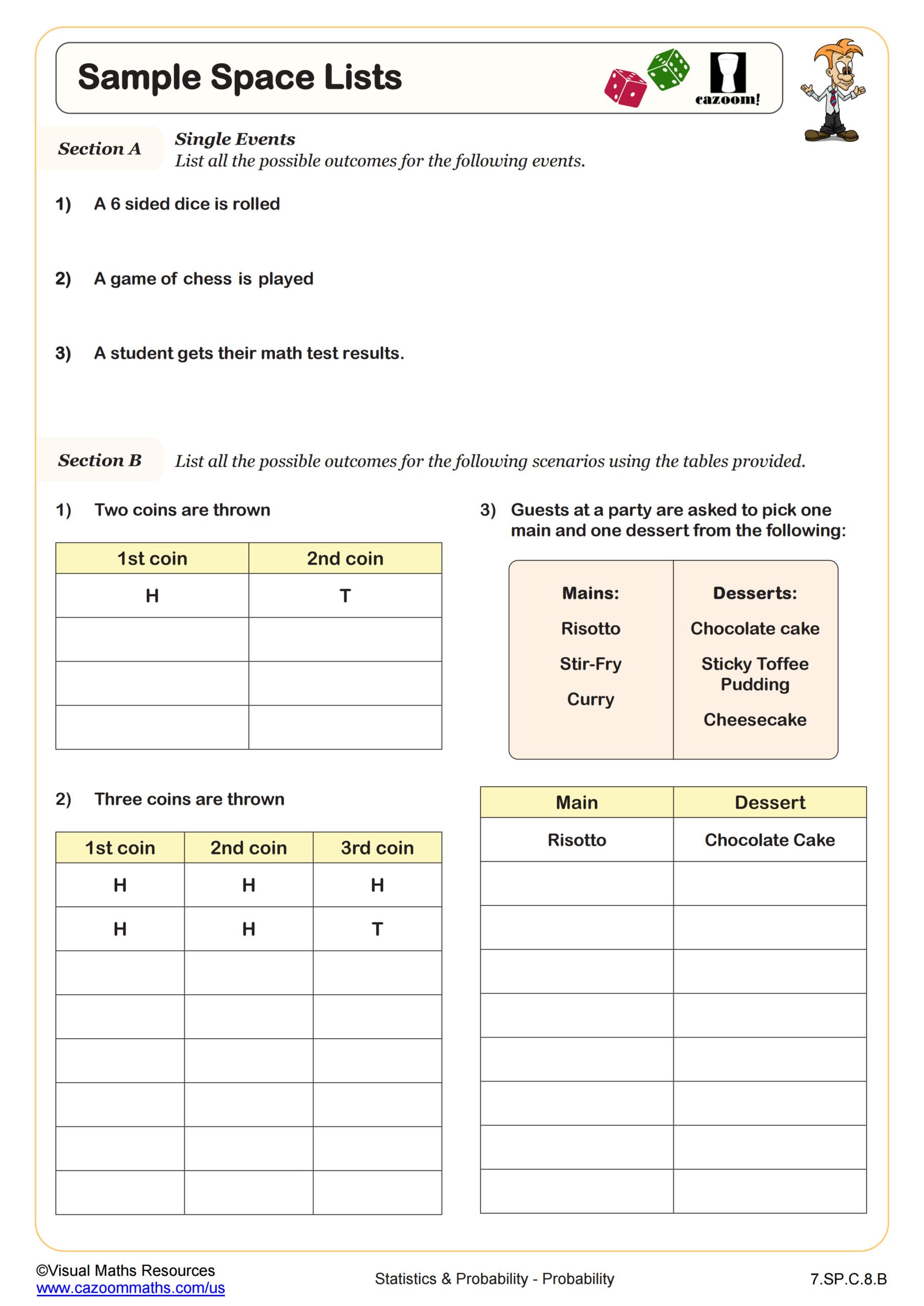
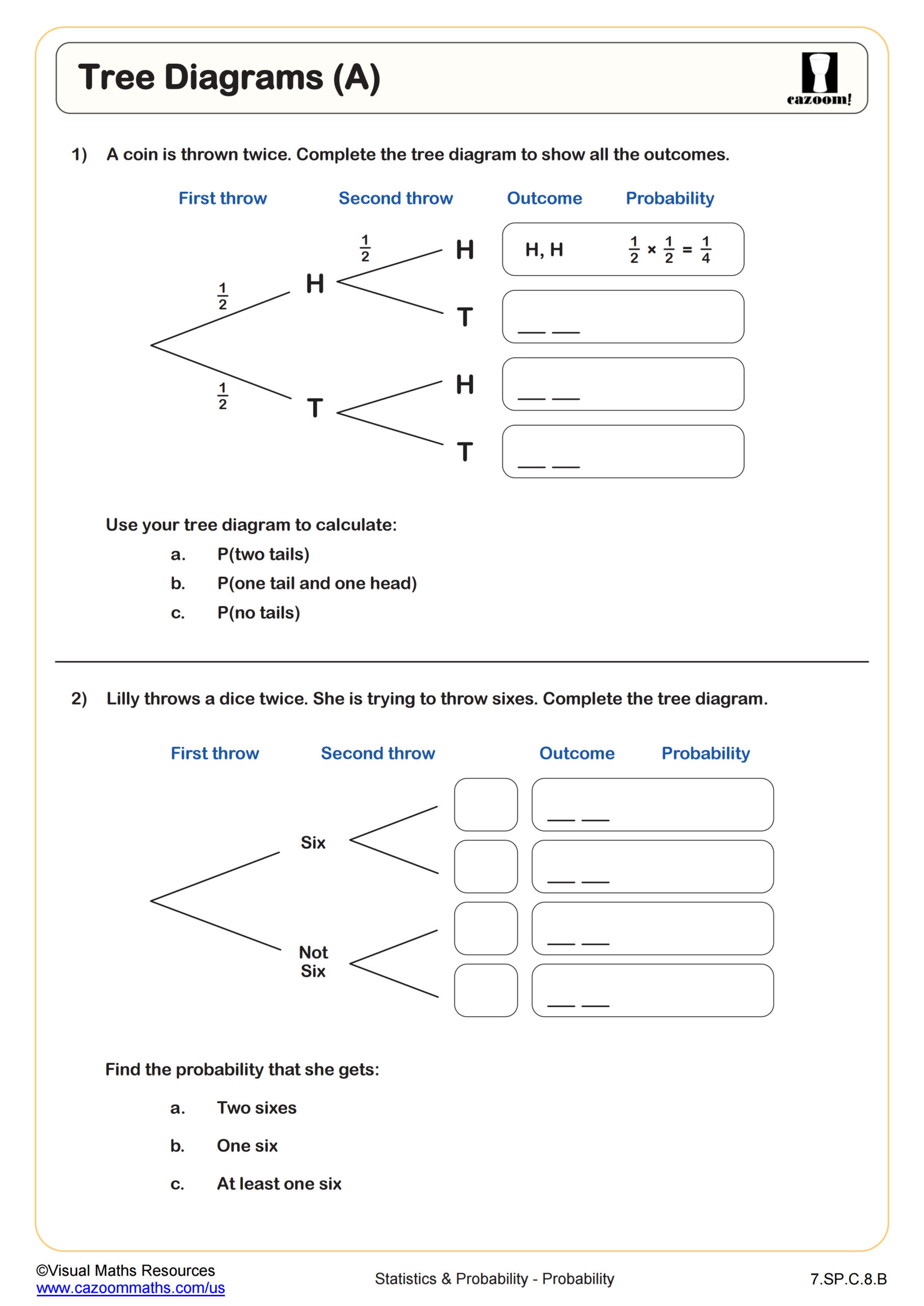
This worksheet provides a comprehensive overview of the probability rule for counting, gradually progressing from basic problems to more complex scenarios. Section A kicks things off by asking students to use a sample space diagram to list all possible outcomes. As the variables change students will consider what impact this has on the total number of outcomes. Then Sections B and C will see students applying the probability rule for counting to solve problems with independent events where order does and does not matter. All questions are based on practical situations such as menu choices and games played in sports leagues.
Students may use calculators while completing this worksheet.