Loading...
Back to:
Time as Fractions (A) WORKSHEET
Suitable for Grades: 5th Grade
CCSS: 5.NF.B.4
CCSS Description: Apply and extend previous understandings of multiplication to multiply a fraction or whole number by a fraction. a. Interpret the product (a/b) × q as a parts of a partition of q into b equal parts; equivalently, as the result of a sequence of operations a × q ÷ b. For example, use a visual fraction model to show (2/3) × 4 = 8/3, and create a story context for this equation. Do the same with (2/3) × (4/5) = 8/15. (In general, (a/b) × (c/d) = ac/bd.) b. Find the area of a rectangle with fractional side lengths by tiling it with unit squares of the appropriate unit fraction side lengths, and show that the area is the same as would be found by multiplying the side lengths. Multiply fractional side lengths to find areas of rectangles, and represent fraction products as rectangular areas.
Time as Fractions (A) WORKSHEET DESCRIPTION
Understanding fractions as lengths of time is often a challenging concept for students to grasp.
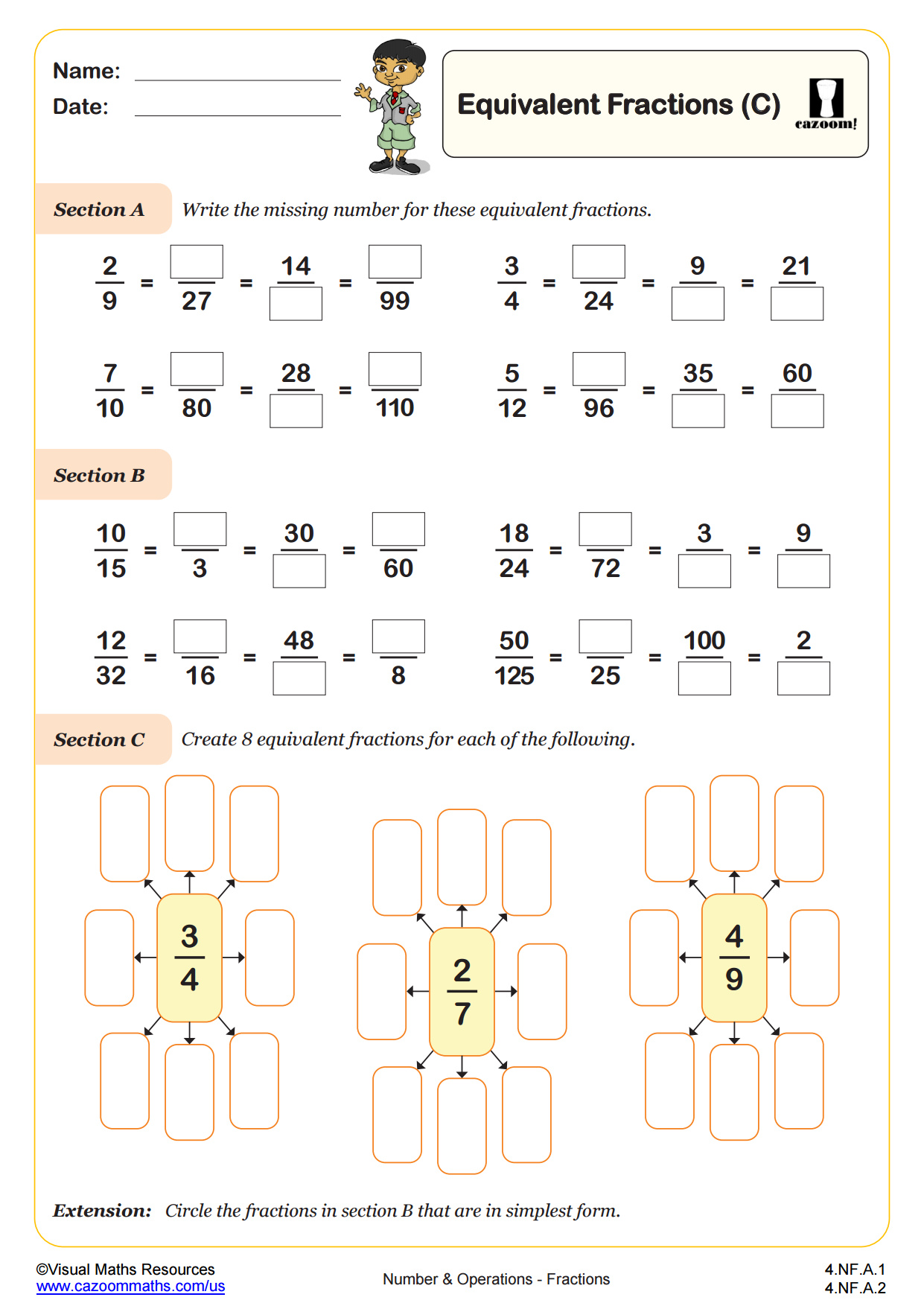
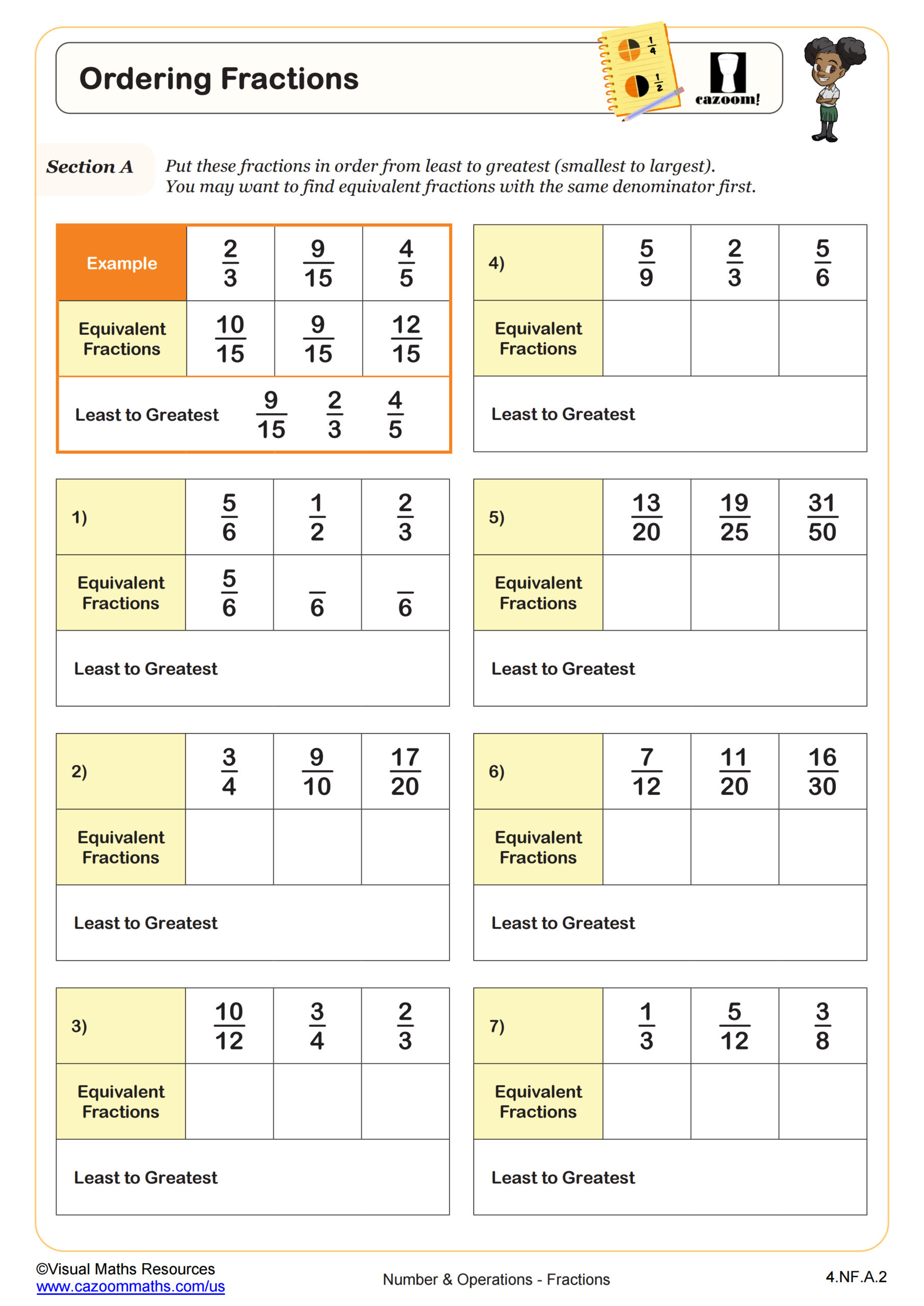
Section A is all about finding fractions of 60. Students are given one example and 5 questions which focus on common fractions of time e.g 1/12.
In section B, learners will interpret their answers from section A by completing sentences such as “½ an hour is 30 minutes because ½ of 60 is 30.”
Next, students will form chains of equivalent fractions with one fraction in each set having a denominator of 60, and again, using their answers, will interpret these fractions as units of time.
Finally, learners are faced with 4 amounts in minutes to write as a fraction of an hour and vice versa. Your learners should be able to choose which of the above methods they prefer to use.
